iT邦幫忙

2017 iT 邦幫忙鐵人賽
DAY 25
2
Modern Web

30天實作線上簡報播放機制系列 第 30 篇

?? - 處理Office的內建圖型

2017鐵人賽 office openxml html5 canvas powerpoint
23933 瀏覽

  • 分享至 

  • xImage
    •  

既然還能發文...

ECMA-376定義Office內建圖型的方法

在規格書的zip檔中，可以找到presetShapeDefinitions.xml這個檔案（應該是在另一個zip檔中），裡面定義了Office內建圖型的繪製方法。

每個圖型的資料大概可以分成幾個部分：

  1. 各個變數的計算方程式
  2. 參數預設值
  3. 參數handler，可以透過他的定義繪出互動式調整參數的介面
  4. 連接點
  5. 圖型內文字方塊的位置
  6. 繪製路徑

以一個向下的箭頭（downArrow）作為例子，他的定義：

<downArrow>
<avLst xmlns="http://schemas.openxmlformats.org/drawingml/2006/main">
  <gd name="adj1" fmla="val 50000" />
  <gd name="adj2" fmla="val 50000" />
</avLst>
<gdLst xmlns="http://schemas.openxmlformats.org/drawingml/2006/main">
  <gd name="maxAdj2" fmla="*/ 100000 h ss" />
  <gd name="a1" fmla="pin 0 adj1 100000" />
  <gd name="a2" fmla="pin 0 adj2 maxAdj2" />
  <gd name="dy1" fmla="*/ ss a2 100000" />
  <gd name="y1" fmla="+- b 0 dy1" />
  <gd name="dx1" fmla="*/ w a1 200000" />
  <gd name="x1" fmla="+- hc 0 dx1" />
  <gd name="x2" fmla="+- hc dx1 0" />
  <gd name="dy2" fmla="*/ x1 dy1 wd2" />
  <gd name="y2" fmla="+- y1 dy2 0" />
</gdLst>
<ahLst xmlns="http://schemas.openxmlformats.org/drawingml/2006/main">
  <ahXY gdRefX="adj1" minX="0" maxX="100000">
    <pos x="x1" y="t" />
  </ahXY>
  <ahXY gdRefY="adj2" minY="0" maxY="maxAdj2">
    <pos x="l" y="y1" />
  </ahXY>
</ahLst>
<cxnLst xmlns="http://schemas.openxmlformats.org/drawingml/2006/main">
  <cxn ang="3cd4">
    <pos x="hc" y="t" />
  </cxn>
  <cxn ang="cd2">
    <pos x="l" y="y1" />
  </cxn>
  <cxn ang="cd4">
    <pos x="hc" y="b" />
  </cxn>
  <cxn ang="0">
    <pos x="r" y="y1" />
  </cxn>
</cxnLst>
<rect l="x1" t="t" r="x2" b="y2" xmlns="http://schemas.openxmlformats.org/drawingml/2006/main" />
<pathLst xmlns="http://schemas.openxmlformats.org/drawingml/2006/main">
  <path>
    <moveTo>
      <pt x="l" y="y1" />
    </moveTo>
    <lnTo>
      <pt x="x1" y="y1" />
    </lnTo>
    <lnTo>
      <pt x="x1" y="t" />
    </lnTo>
    <lnTo>
      <pt x="x2" y="t" />
    </lnTo>
    <lnTo>
      <pt x="x2" y="y1" />
    </lnTo>
    <lnTo>
      <pt x="r" y="y1" />
    </lnTo>
    <lnTo>
      <pt x="hc" y="b" />
    </lnTo>
    <close />
  </path>
</pathLst>
</downArrow>

在變數計算的部份，有很多<gd>元素，他的name屬性就是在定義中使用的變數名稱，fmla屬性則是以前序式定義的計算方法。

例如<gd name="dy1" fmla="*/ ss a2 100000" />，就是定義一個變數，名稱是dy1，計算方式是：ss*a2/100000。其中ss及a2是這個計算方程式中會使用的其他變數。

有一些系統預設的變數沒有定義在這裡，而是定義在ECMA-376 Edition 5 Part 1的「20.1.10.56 ST_ShapeType (Preset Shape Types)」這一節中。另外，這些方程式的語法定義，可以從ECMA-376 Edition 5 Part 1的「20.1.9.11 gd (Shape Guide)」這一節找到。如果像要看個別的說明，請參考規格書。

處理計算及繪製

最早做概念驗證的時候，是靠人力把這些定義轉成程式...不過這樣當然無法應付實際使用的狀況。另外，投影片中有些圖型是使用者自己定義的，這些圖型也是用一樣的方法定義，而且需要被動態繪製出來，所以需要有一個方法來剖析這些定義。

實際上規格書中定義的方程式只有17種，這些計算方式也不複雜，所以各位一種方程式定義一個函數，就可以應付了。另外，也需要把變數集中管理，隨者計算的過程，動態產生計算好的變數。

為了應付這樣的計算，寫一個簡單的Javascript constructor來產生物件：

function Guides(ctx, w, h, _c) {
  if(!!_c && typeof _c === 'function') {
    this.conv = _c;
  } else {
    if(!!emu2pixel && typeof emu2pixel === 'function') this.conv = emu2pixel;
    this.conv = function(n){return n};
  }
  this.w = w;
  this.h = h;
  this.l = 0;
  this.t = 0;
  this['3cd4'] = 16200000;
  this['3cd8'] = 8100000;
  this['5cd8'] = 13500000;
  this['7cd8'] = 18900000;
  this.b = h;
  this.r = w;
  this.cd2 = 10800000;
  this.cd4 = 5400000;
  this.cd8 = 2700000;
  this.factor = 2 * Math.PI / 21600000;
  parse.call(this, 'hc', '*/ w 1 2');
  parse.call(this, 'hd2', '*/ h 1 2');
  parse.call(this, 'hd3', '*/ h 1 3');
  parse.call(this, 'hd4', '*/ h 1 4');
  parse.call(this, 'hd5', '*/ h 1 5');
  parse.call(this, 'hd6', '*/ h 1 6');
  parse.call(this, 'hd8', '*/ h 1 8');
  parse.call(this, 'ls', 'max w h');
  parse.call(this, 'ss', 'min w h');
  parse.call(this, 'ssd2', '*/ ss 1 2');
  parse.call(this, 'ssd4', '*/ ss 1 4');
  parse.call(this, 'ssd6', '*/ ss 1 6');
  parse.call(this, 'ssd8', '*/ ss 1 8');
  parse.call(this, 'ssd16', '*/ ss 1 16');
  parse.call(this, 'ssd32', '*/ ss 1 32');
  parse.call(this, 'vc', '*/ h 1 2');
  parse.call(this, 'wd2', '*/ w 1 2');
  parse.call(this, 'wd3', '*/ w 1 3');
  parse.call(this, 'wd4', '*/ w 1 4');
  parse.call(this, 'wd5', '*/ w 1 5');
  parse.call(this, 'wd6', '*/ w 1 6');
  parse.call(this, 'wd8', '*/ w 1 8');
  parse.call(this, 'wd10', '*/ 1 10');

  this.addFormula = function(name, fmla) {
    parse.call(this, name, fmla);
  };

  this.lineTo = function(x, y) {
    ctx.lineTo(this.conv(x), this.conv(y));
  }

  this.moveTo = function(x, y) {
    ctx.moveTo(this.conv(x), this.conv(y));
  }

  this.begin = function() {
    ctx.beginPath();
  }

  this.close = function() {
    ctx.closePath();
  }

  this.arcTo = function(hr, vr, sta, swa, curx, cury) {
    if(swa < 0) {
      if((sta + swa) < 0) {
        var start = sta + swa + 21600000;
      } else {
        var start = sta + swa;
      }
      var end = sta;
    } else {
      var start = sta;
      var end = sta + swa;
    }
    var ecx = curx - hr * Math.cos(sta * 2 * Math.PI / 21600000);
    var ecy = cury - vr * Math.sin(sta * 2 * Math.PI / 21600000);
    if(swa < 0) {
      var tx = ecx + hr * Math.cos(start * 2 * Math.PI / 21600000);
      var ty = ecy + vr * Math.sin(start * 2 * Math.PI / 21600000);
      ctx.moveTo(this.conv(tx), this.conv(ty));
    }
    ctx.ellipse(this.conv(ecx), this.conv(ecy), this.conv(hr), this.conv(vr), 0, start * 2 * Math.PI / 21600000, end * 2 * Math.PI / 21600000);
    if(swa < 0) {
      ctx.moveTo(this.conv(tx), this.conv(ty));
        return {x:tx, y:ty};
    } else {
      var tx = ecx + hr * Math.cos(end * 2 * Math.PI / 21600000);
      var ty = ecy + vr * Math.sin(end * 2 * Math.PI / 21600000);
      return {x:tx,y:ty};
    }
  }

  function parse(name, fmla) {
    var key = fmla.split(/[ ]+/)[0];
    var args = fmla.split(/[ ]+/).slice(1);
    var circle = 21600;
    var factor = 2 * Math.PI / circle;
    var formulas = {
      "+-": function(a, b, c) {
        return a + b - c;
      },
      "+/": function(a, b, c) {
        return (a + b) / c;
      },
      "*/": function(a, b, c) {
        return a * b / c;
      },
      "?:": function(a, b, c) {
        return a>0?b:c;
      },
      "abs": function(a) {
        return Math.abs(a);
      },
      "at2": function(a, b) {
        return Math.atan(b/a*factor);
      },
      "cat2": function(a, b, c) {
        return a * Math.cos(Math.atan(c/b*factor)*factor);
      },
      "cos": function(a, b) {
        return a * Math.cos(b*factor);
      },
      "max": function(a, b) {
        return a>b?a:b;
      },
      "min": function(a, b) {
        return a>b?b:a;
      },
      "mod": function(a, b, c) {
        return Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2) + Math.pow(c, 2));
      },
      "pin": function(a, b, c) {
        return b<a?a:b>c?c:b;
      },
      "sat2": function(a, b, c) {
        return a * Math.sin(Math.atan(c/b*factor)*factor);
      },
      "sin": function(a, b) {
        return a * Math.sin(b*factor);
      },
      "sqrt": function(a) {
        return Math.sqrt(a);
      },
      "tan": function(a, b) {
        return a * Math.tan(b*factor);
      },
      "val": function(a) {
        if(isNaN(parseInt(a, 10))) return a;
        return parseInt(a, 10);
      }
    };
    var that = this;
    var _args = args.reduce(function(pre, cur) {
      if(isNaN(parseInt(cur, 10))) {
        pre.push(that[cur]);
      } else {
        pre.push(parseInt(cur, 10));
      }
      return pre;
    }, []);
    if(!!formulas[key]) {
      this[name] = formulas[key].apply(this, _args);
    } else {
      throw "Operator or function not supported.";
    }
  }
}

所有的系統預設變數都放進去了，這樣就不需要回頭翻規格書。使用的時候，傳給他canvas 2d context、圖型的寬高、以及單位轉換函數，來產生實例：

var gd = new Guides(ctx, shape.cx, shape.cy, emu2pixel);
shape.presetGeom.avList.forEach(function(a) {
  gd.addFormula(a.name, a.fmla);
});

以我的例子，圖型的參數會放在shape.presetGeom.avList中，只要迭代一下把它的變數名稱及計算方式傳給addFormula方法，這個變數就會加到gd物件中。如果加入的是adj1，那只要透過gd.adj1就可以取用。

以前面的downArrow為例，計算過程就像這樣：

var gd = new Guides(ctx, shape.cx, shape.cy, emu2pixel);
shape.presetGeom.avList.forEach(function(a) {
  gd.addFormula(a.name, a.fmla);
})

gd.addFormula('maxAdj2', '*/ 100000 h ss');
gd.addFormula('a1', 'pin 0 adj1 100000');
gd.addFormula('a2', 'pin 0 adj2 maxAdj2');
gd.addFormula('dy1', '*/ ss a2 100000');
gd.addFormula('y1', '+- b 0 dy1');
gd.addFormula('dx1', '*/ w a1 200000');
gd.addFormula('x1', '+- hc 0 dx1');
gd.addFormula('x2', '+- hc dx1 0');
gd.addFormula('dy2', '*/ x1 dy1 wd2');
gd.addFormula('y2', '+- y1 dy2 0');

presetShapeDefinitions.xml中定義的計算過程是依照需要的順序的，所以就把他們依照文件中的定義寫到程式中。所有使用到的變數處理完後，屆下來就需要繪製。

繪製的方法定義在<pathLst>中，裡面定義了幾種操作。對downArrow圖型來說其實很簡單，一開始移到定點後，接下來就是對計算好的座標繪製直線。轉成程式的話：

gd.moveTo(gd.l, gd.y1);
gd.begin();
gd.lineTo(gd.x1, gd.y1);
gd.lineTo(gd.x1, gd.t);
gd.lineTo(gd.x2, gd.t);
gd.lineTo(gd.x2, gd.y1);
gd.lineTo(gd.r, gd.y1);
gd.lineTo(gd.hc, gd.b);
gd.lineTo(gd.l, gd.y1);
gd.close();

這樣就可以繪製出路徑。根據圖型中的資料設定好填色及邊框的繪製方式以及顏色，就可以把圖形畫出來。繪製出來的向下箭頭像這張圖中投影片使用的：

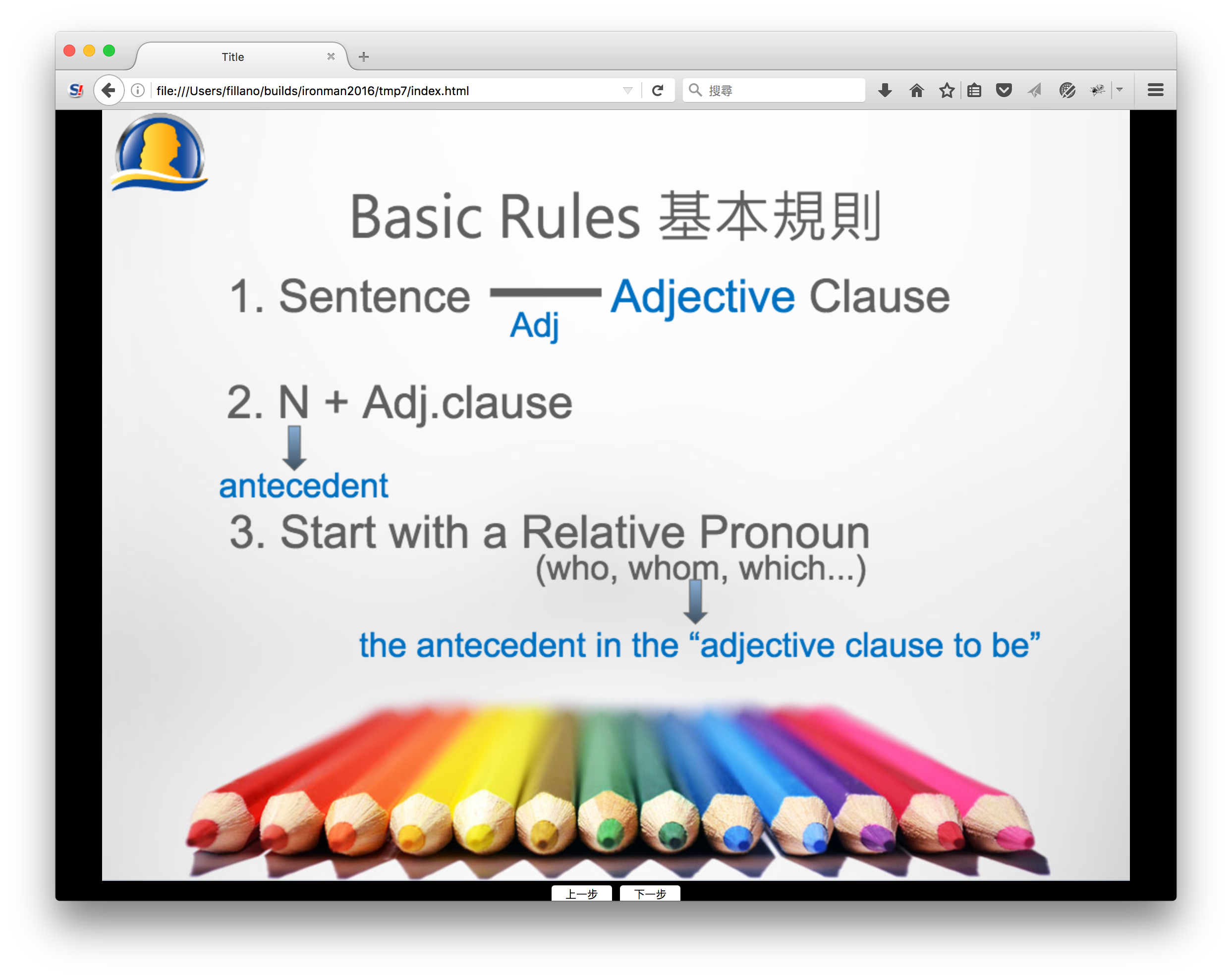
99-004.png

文件中還定義了幾種路徑繪製方式，例如arcTo。比較大的問題是，他跟HTML5 Canvas 2D Context API的arcTo介面不一樣，使用方式甚至會有一些衝突。Canvas的arcTo目前只能繪製正圓的圓弧，ECMA-376使用的則可以繪製橢圓。使用Canvas的ellipse方法的話，會碰到另一個問題...因為在Canvas的ellipse方法中，所要繪製圓弧的角度從起點到終點必須依照「順時針」的方向指定，所以在ECMA-376中定義的弧線，轉到Canvas中繪製，可能需要從終點繪製回來...這當中需要用moveTo方法移動兩次，否則關閉路徑時會跑出額外的東西XD。在Guides中也定義了arcTo方法，稍微包裝一下這個過程。但是實際繪製時，會需要知道繪製起點的座標，並且回傳終點的座標。如果arcTo的前個操作是lineTo或moveTo的話是沒問題；如果前個操作也是arcTo的話，根本不會知道起點在哪裡，所以只好加了兩個參數進去。

預設圖型中的大括號，繪製時就會使用到弧線。目前使用的繪製方式：

var gd = new Guides(ctx, shape.cx, shape.cy, emu2pixel);
shape.presetGeom.avList.forEach(function(a) {
  gd.addFormula(a.name, a.fmla);
});

gd.addFormula('a2', 'pin 0 adj2 100000');
gd.addFormula('q1', '+- 100000 0 a2');
gd.addFormula('q2', 'min q1 a2');
gd.addFormula('q3', '*/ q2 1 2');
gd.addFormula('maxAdj1', '*/ q3 h ss');
gd.addFormula('a1', 'pin 0 adj1 maxAdj1');
gd.addFormula('y1', '*/ ss a1 100000');
gd.addFormula('y3', '*/ h a2 100000');
gd.addFormula('y4', '+- y3 y1 0');
gd.addFormula('dx1', 'cos wd2 2700000');
gd.addFormula('dy1', 'sin y1 2700000');
gd.addFormula('il', '+- r 0 dx1');
gd.addFormula('it', '+- y1 0 dy1');
gd.addFormula('ib', '+- b dy1 y1');

gd.moveTo(gd.r, gd.b);
gd.begin();
gd.arcTo(gd.wd2, gd.y1, gd.cd4, gd.cd4, gd.r, gd.b);
gd.lineTo(gd.hc, gd.y4);
var t1 = gd.arcTo(gd.wd2, gd.y1, 0, -5400000, gd.hc, gd.y4);
gd.arcTo(gd.wd2, gd.y1, gd.cd4, -5400000, t1.x, t1.y);
gd.lineTo(gd.hc, gd.y1);
gd.arcTo(gd.wd2, gd.y1, gd.cd2, gd.cd4, gd.hc, gd.y1);

畫出來的效果：

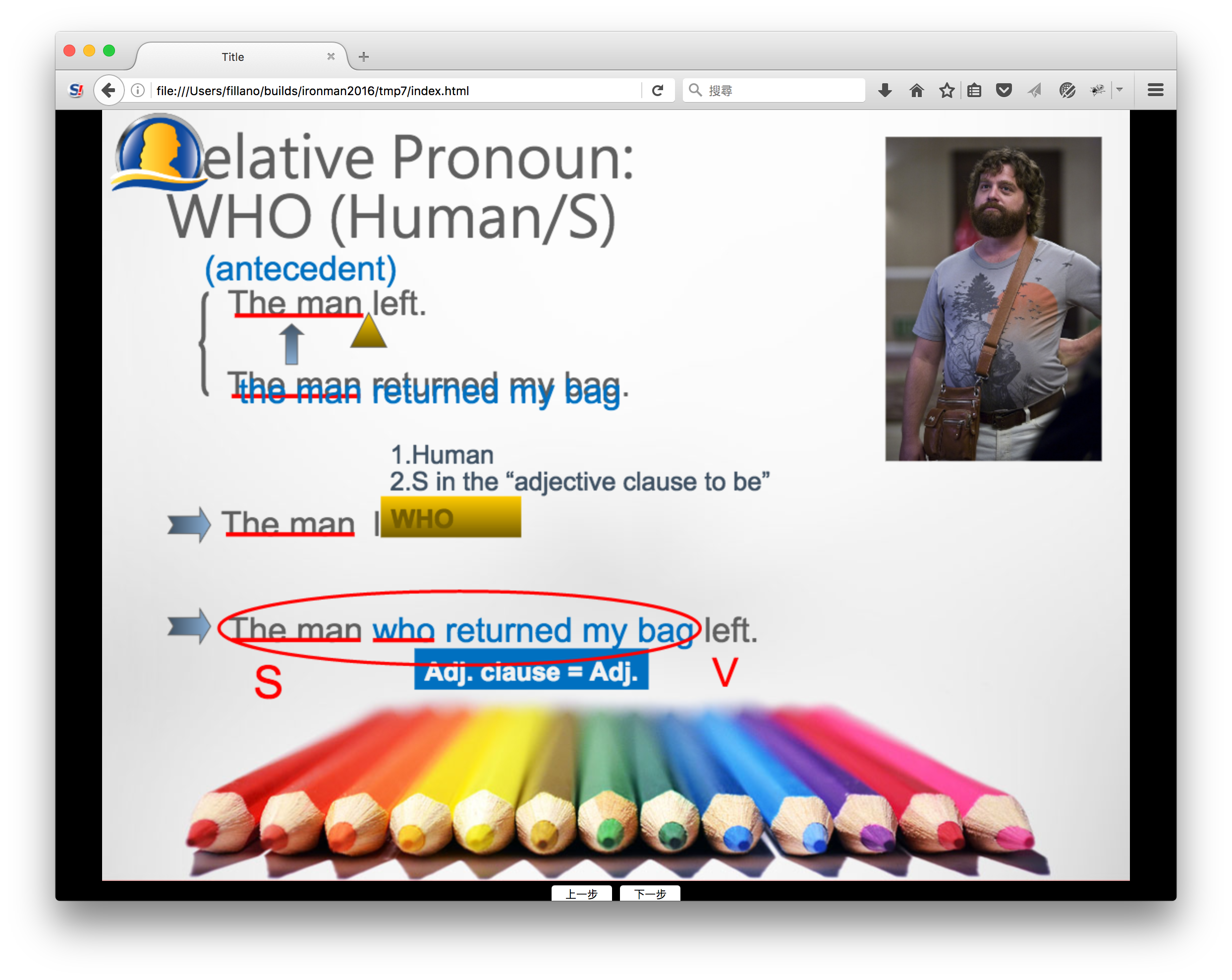
99-005.png

裡面還有其他圖型，就不多提了。

實際在繪製客製化圖型時，還會有其他繪製方法需要實作，希望跟Canvas的API不要差太多，不然光是大括號就花了一些時間XD

一些小坑

ECMA-376定義圖型有一些假設，最重要的是，圖型的圓點在(0, 0)。所以gd.l跟gd.t這兩個變數都是0。在實作時，需要先用ctx.translate()移動canvas，畫好以後再移回來。雖然沒解釋，但是規格書內都有寫。沒有參透這個，我還以為presetShapeDefinitions.xml中的定義有錯誤...

另外，為了可以在計算過程中產生計算好的變數，用了物件導向的寫法...然後就碰到this的問題...

小結一下

賽程中斷後雖然還有寫文章，但是加起來只有29篇。既然鐵人賽按鈕還在，就加一篇補足30篇吧...


上一篇
?? - 雖然沒完賽，還是發一下心得
下一篇
?? - 目前初步做好的prototype
系列文
30天實作線上簡報播放機制 共 31 篇
  1. 27
    ?? - 目前的簡單成果
  2. 28
    ?? - 繪製Office內建的圖型
  3. 29
    ?? - 雖然沒完賽，還是發一下心得
  4. 30
    ?? - 處理Office的內建圖型
  5. 31
    ?? - 目前初步做好的prototype
完整目錄
圖片
  直播研討會
圖片
{{ item.channelVendor }} {{ item.webinarstarted }} |
{{ formatDate(item.duration) }}
直播中

2 則留言

0
海綿寶寶
iT邦大神 1 級 ‧ 2017-01-20 18:41:53

不懂純推
/images/emoticon/emoticon12.gif/images/emoticon/emoticon12.gif/images/emoticon/emoticon12.gif

登入發表回應
1
fillano
iT邦超人 1 級 ‧ 2017-01-23 10:57:55

Guides的程式有一些改進，所以再補充一下：

  1. ctx.ellipse()有一個optional的參數，指定繪圖的方向是否為逆時針。所以把它實作到Guides.arcTo()方法裡面。
  2. 既然把ctx傳給Guides讓他繪圖，一些繪圖的狀態其實可以由Guides自己管理，例如目前的位置。這樣Guides.arcTo()就不需要傳給他目前位置，也不用返回目前位置。透過這個修改，arcTo的介面就跟ECMA-376一致了。
function Guides(ctx, w, h, _c) {
	if(!!_c && typeof _c === 'function') {
		this.conv = _c;
	} else {
		if(!!emu2pixel && typeof emu2pixel === 'function') this.conv = emu2pixel;
		this.conv = function(n){return n};
	}
	var cur = {x:0,y:0};
	this.w = w;
	this.h = h;
	this.l = 0;
	this.t = 0;
	this['3cd4'] = 16200000;
	this['3cd8'] = 8100000;
	this['5cd8'] = 13500000;
	this['7cd8'] = 18900000;
	this.b = h;
	this.r = w;
	this.cd2 = 10800000;
	this.cd4 = 5400000;
	this.cd8 = 2700000;
	this.factor = 2 * Math.PI / 21600000;
	parse.call(this, 'hc', '*/ w 1 2');
	parse.call(this, 'hd2', '*/ h 1 2');
	parse.call(this, 'hd3', '*/ h 1 3');
	parse.call(this, 'hd4', '*/ h 1 4');
	parse.call(this, 'hd5', '*/ h 1 5');
	parse.call(this, 'hd6', '*/ h 1 6');
	parse.call(this, 'hd8', '*/ h 1 8');
	parse.call(this, 'ls', 'max w h');
	parse.call(this, 'ss', 'min w h');
	parse.call(this, 'ssd2', '*/ ss 1 2');
	parse.call(this, 'ssd4', '*/ ss 1 4');
	parse.call(this, 'ssd6', '*/ ss 1 6');
	parse.call(this, 'ssd8', '*/ ss 1 8');
	parse.call(this, 'ssd16', '*/ ss 1 16');
	parse.call(this, 'ssd32', '*/ ss 1 32');
	parse.call(this, 'vc', '*/ h 1 2');
	parse.call(this, 'wd2', '*/ w 1 2');
	parse.call(this, 'wd3', '*/ w 1 3');
	parse.call(this, 'wd4', '*/ w 1 4');
	parse.call(this, 'wd5', '*/ w 1 5');
	parse.call(this, 'wd6', '*/ w 1 6');
	parse.call(this, 'wd8', '*/ w 1 8');
	parse.call(this, 'wd10', '*/ 1 10');

	this.addFormula = function(name, fmla) {
		parse.call(this, name, fmla);
	};

	this.lineTo = function(x, y) {
		ctx.lineTo(this.conv(x), this.conv(y));
		cur.x = x, cur.y = y;
	}

	this.moveTo = function(x, y) {
		ctx.moveTo(this.conv(x), this.conv(y));
		cur.x = x, cur.y = y;
	}

	this.begin = function() {
		ctx.beginPath();
	}

	this.close = function() {
		ctx.closePath();
	}

	this.arcTo = function(hr, vr, sta, swa) {
		if(swa < 0) {
			var anticlock = true;
			if(sta + swa < 0) {
				var end = sta + swa + 21600000;
			} else {
				var end = sta + swa;
			}
		} else {
			var anticlock = false;
			var end = sta + swa;
		}
		var ecx = cur.x - hr * Math.cos(sta * 2 * Math.PI / 21600000);
		var ecy = cur.y - vr * Math.sin(sta * 2 * Math.PI / 21600000);
		ctx.ellipse(this.conv(ecx), this.conv(ecy), this.conv(hr), this.conv(vr), 0, sta * 2 * Math.PI / 21600000, end * 2 * Math.PI / 21600000, anticlock);
		cur.x = ecx + hr * Math.cos(end * 2 * Math.PI / 21600000);
		cur.y = ecy + vr * Math.sin(end * 2 * Math.PI / 21600000);
	}

	function parse(name, fmla) {
		var key = fmla.split(/[ ]+/)[0];
		var args = fmla.split(/[ ]+/).slice(1);
		var circle = 21600;
		var factor = 2 * Math.PI / circle;
		var formulas = {
			"+-": function(a, b, c) {
				return a + b - c;
			},
			"+/": function(a, b, c) {
				return (a + b) / c;
			},
			"*/": function(a, b, c) {
				return a * b / c;
			},
			"?:": function(a, b, c) {
				return a>0?b:c;
			},
			"abs": function(a) {
				return Math.abs(a);
			},
			"at2": function(a, b) {
				return Math.atan(b/a*factor);
			},
			"cat2": function(a, b, c) {
				return a * Math.cos(Math.atan(c/b*factor)*factor);
			},
			"cos": function(a, b) {
				return a * Math.cos(b*factor);
			},
			"max": function(a, b) {
				return a>b?a:b;
			},
			"min": function(a, b) {
				return a>b?b:a;
			},
			"mod": function(a, b, c) {
				return Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2) + Math.pow(c, 2));
			},
			"pin": function(a, b, c) {
				return b<a?a:b>c?c:b;
			},
			"sat2": function(a, b, c) {
				return a * Math.sin(Math.atan(c/b*factor)*factor);
			},
			"sin": function(a, b) {
				return a * Math.sin(b*factor);
			},
			"sqrt": function(a) {
				return Math.sqrt(a);
			},
			"tan": function(a, b) {
				return a * Math.tan(b*factor);
			},
			"val": function(a) {
				if(isNaN(parseInt(a, 10))) return a;
				return parseInt(a, 10);
			}
		};
		var that = this;
		var _args = args.reduce(function(pre, cur) {
			if(isNaN(parseInt(cur, 10))) {
				pre.push(that[cur]);
			} else {
				pre.push(parseInt(cur, 10));
			}
			return pre;
		}, []);
		if(!!formulas[key]) {
			this[name] = formulas[key].apply(this, _args);
		} else {
			throw "Operator or function not supported.";
		}
	}
}

透過這個修改，自定圖形的繪製會比較簡單，不用再判斷使用的繪製方法。只是在實作任何繪製方法時，都需要把目前的位置更新。還需要實作的是cubicBezTo方法（cubic beizier curve to）

登入發表回應

我要留言

立即登入留言
iThome鐵人賽
參賽組數
1064 組
團體組數
40 組
累計文章數
22183 篇
完賽人數
597 人
iT+看影片追技術 看影片追技術 看更多
熱門tag 看更多
15th鐵人賽 16th鐵人賽 13th鐵人賽 14th鐵人賽 12th鐵人賽 11th鐵人賽 鐵人賽 2019鐵人賽 javascript 2018鐵人賽 python 2017鐵人賽 windows php c# windows server linux css react vue.js
熱門問題
熱門回答
熱門文章
IT邦幫忙